Tugas 2 Teknik Riset Operasi

 

1. Diketahui :
Minimasi : Z= 6 X1 + 7,5 X2
Dengan fungsi pembatas :
7X1 + 3X2 ≥ 210
6X1 + 12X2  ≥ 180
4X2 ≥ 120
X1 , X2 ≥ 0
Ditanyakan : Berapakah  nilai X1 dan X2?
Jawab :
Bentuk standar dari fungsi z adalah:
Z – 6X1 – 7,5X2 = 0
Jika sema fungsi yang ada diurutkan:

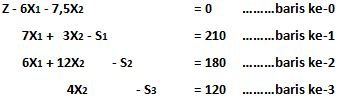
Untuk minimasi, syarat pertama adalah variable non basis pada baris ke-0 harus semuanya negatif, karena baris ke-0 sudah memenuhi syarat minimasi yang optimal, jadi tidak perlu dilakukan iterasi.
Tabel awal:

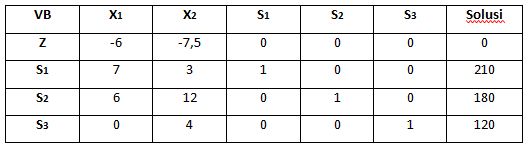
Dari table di atas yang sudah optimum, dapat disimpulkan bahwa:

• Nilai solusi minimum adalah 0,
• Dengan nilai X1 dan X2 adalah 0.

2. Diketahui :
dimisalkan a = produksi sabun bubuk, dan b = produksi sabun batang
Z = 3a + 2b, dimana Z adalah keuntungan produksi maksimum.
Dengan pembatas : 2a + 5b ≤ 200 ; 6a + 3b ≤ 360 ; a,b ≥ 0
Ditanyakan : Berapa kg jumlah sabun bubuk dan batang yang sebaiknya dibuat?
Jawab :
Bentuk standar:

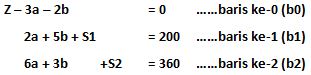
Jika diterapkan pada table dan menggunakan metode eliminasi Gauss Jordan:
Iterasi ke-0 (table awal):

Kolom a NBV yang dijadikan patokan dan baris S2 adalah baris yang NBV a-nya dijadikan 1, karena memiliki nilai rasio terkecil, maka b2 menjadi:
a + 1/2b +1/6S2 = 60
Baris ke-0 dan baris ke-1, NBV a-nya dijadikan 0, menjadi:
Untuk b0, dengan rumus 2b0 + b2, jadi:
-b + 3S2 = 360
Untuk b1, dengan rumus 3b1 – b2, jadi:
12b + 3S1 – S2 = 240
Baris ke-2 (S2) adalah variabel keluar, dan kolom a adalah variable masuk.

Iterasi ke-1:

Kolom b NBV yang dijadikan patokan dan baris S1 adalah baris yang NBV b-nya dijadikan 1, karena memiliki nilai rasio terkecil, maka b1 menjadi:
b + 1/4S1 – 1/12S2 = 20
Baris ke-0 dan baris ke-2, NBV b-nya dijadikan 0, menjadi:
Untuk b0, dengan rumus 12b0 + b1, jadi:
3S1 + 35S2 = 4560
Untuk b2, dengan rumus 24b1 – b1, jadi:
24a + 3S1 + 5S2 = 1200
untuk menjaga NBV a tetap 1, maka dibagi 24, menjadi:
a – 1/8S1 + 5/24 S2 = 50
Baris ke-1 (S1) adalah variabel keluar, dan kolom b adalah variable masuk.
Iterasi ke-2:

Dilihat dari table iterasi ke-2, iterasi diberhentikan, karena baris ke-0 sudah optimal, table sudah optimal dan memenuhi syarat, yaitu sudah tidak ada lagi NBV yang bernilai negatif. Jadi dari table di atas dapat disimpulkan bahwa:

• Nilai maksimum dari produksi sabun bubuk dan sabun batang adalah 4560,
• Dengan nilai a (produksi sabun bubuk) adalah 50,
• Dan nilai b (produksi sabun batang) adalah 20.